Time in Distributed Systems

Primarily we will talk about logical clocks in this post. But let’s first get physical clocks out of the way.

Physical clocks are either time of day and monotonic clocks. Time of day clocks (e.g. Java’s System.currentTimeMillis()) aren’t very useful in distributed systems. Keeping them in sync across the nodes is not easy. Some options like NTP- network time protocol- servers exist.
Monotonic clocks (e.g. Java’s System.nanotime()) are also not very useful. They generally measure time relative to some event (server started). But can go away easily when the node is restarted. And again, they are not useful across nodes or services.

Logical clocks are useful. But not for knowing exact time. The problem logical clocks try to solve is not of an exact epoch. But that of deciding which event took place before which other event. For example, did a read request on a database read replica took place before update request on the same value was placed by another client?

In fact the problem of time in distributed system is mainly the problem of ordering of events. Of course time of day clocks are required. In cases like a sale starts on 00:00hrs GMT. For that physical clocks, barriers, etc. are useful.
But for ordering of events- or determining the order of events- logical clocks are useful.

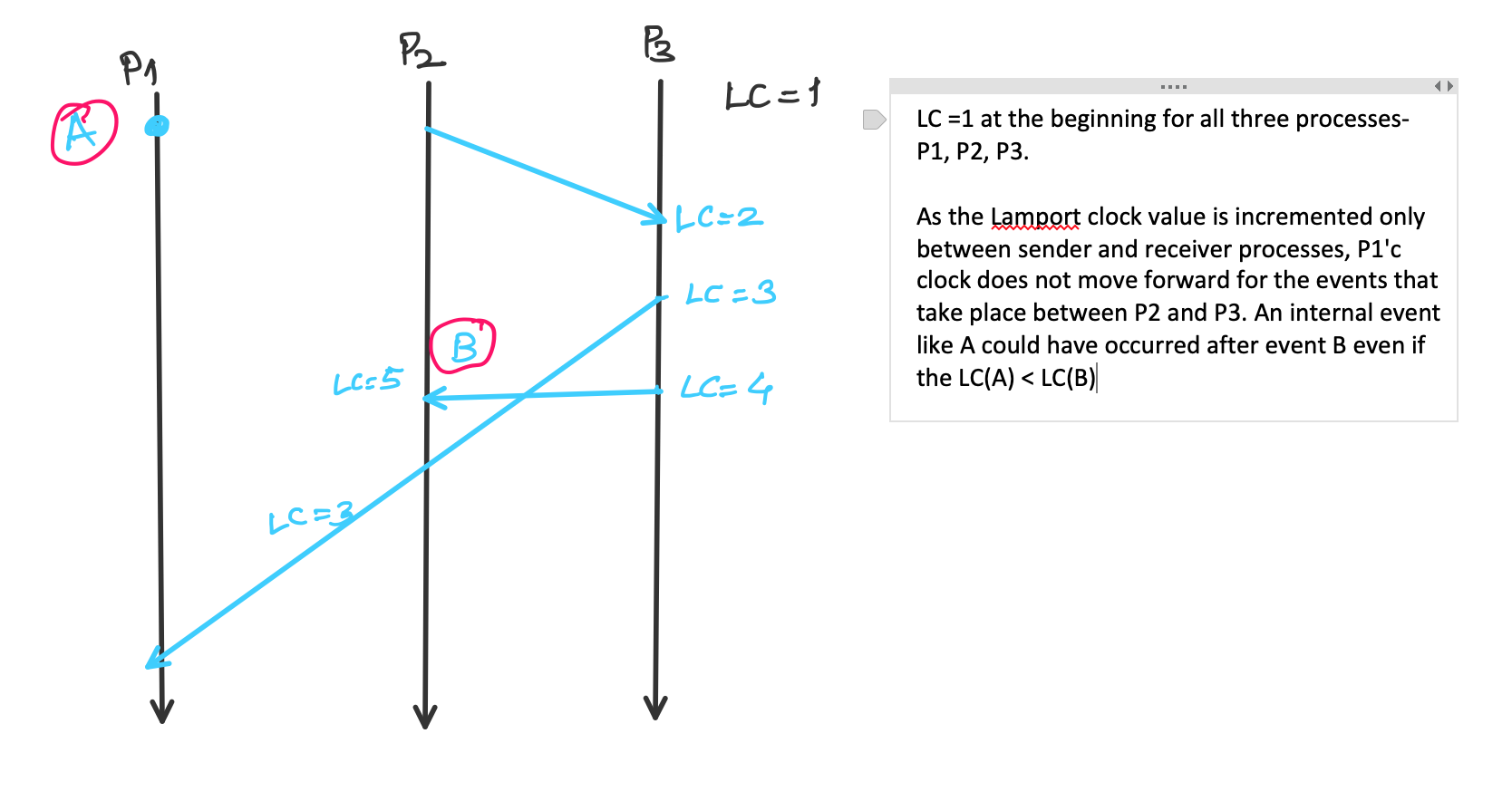
In the area of logical clocks, Lamport clocks are the first. They are simpler and help in partial ordering. But they are useful only so much. For example, we can say that if A happened before B, then Lamport clock of A- denoted here as LC(A)- would be less than LC(B); but we can not for certain say that if LC(A) < LC(B) then A necessarily happened before B. Here I will not detail out the mechanism of how the clock values are sent, used, incremented. It should be apparent from the diagram below. Even if it’s not, let’s move on to vector clocks.

Vector clocks give these guarantees. So

1. if an event A happened before B (that is A -> B), then VC(A) < VC(B), and

2. if VC(A) < VC(B) then it necessarily means that A -> B.

The mechanism of vector clocks is:

1. Every node or process will keep a vector of natural numbers (non-negative ints). These integers are initialized to zeros. For a three process system the vector would be [0,0,0].

2. When a process encounters an event (internal, generated or external)- that is it sends or receives an event, then it increments the number at its own position by one.

3. A process sending an event to another process sends its vector clock to the receiving process along with the event after incrementing its own position. So if P1 sends the first event to P2 then it will send the vector [1,0,0] along with that. If it sends another event to P2 or P3 then it will send [2,0,0] along with that.

4. When a process receives a message/ event, it first increments its own local vector clock position. Then it takes position-wise maximum of the two vector clocks- its local VC and the one incoming with the event. So if P2 had a VC [5, 10, 6] when it received an event from P3 with [9, 8, 8], then the resultant VC at P2 after receiving the event will be [9, 11, 8].

A system with three processes using vector clocks:

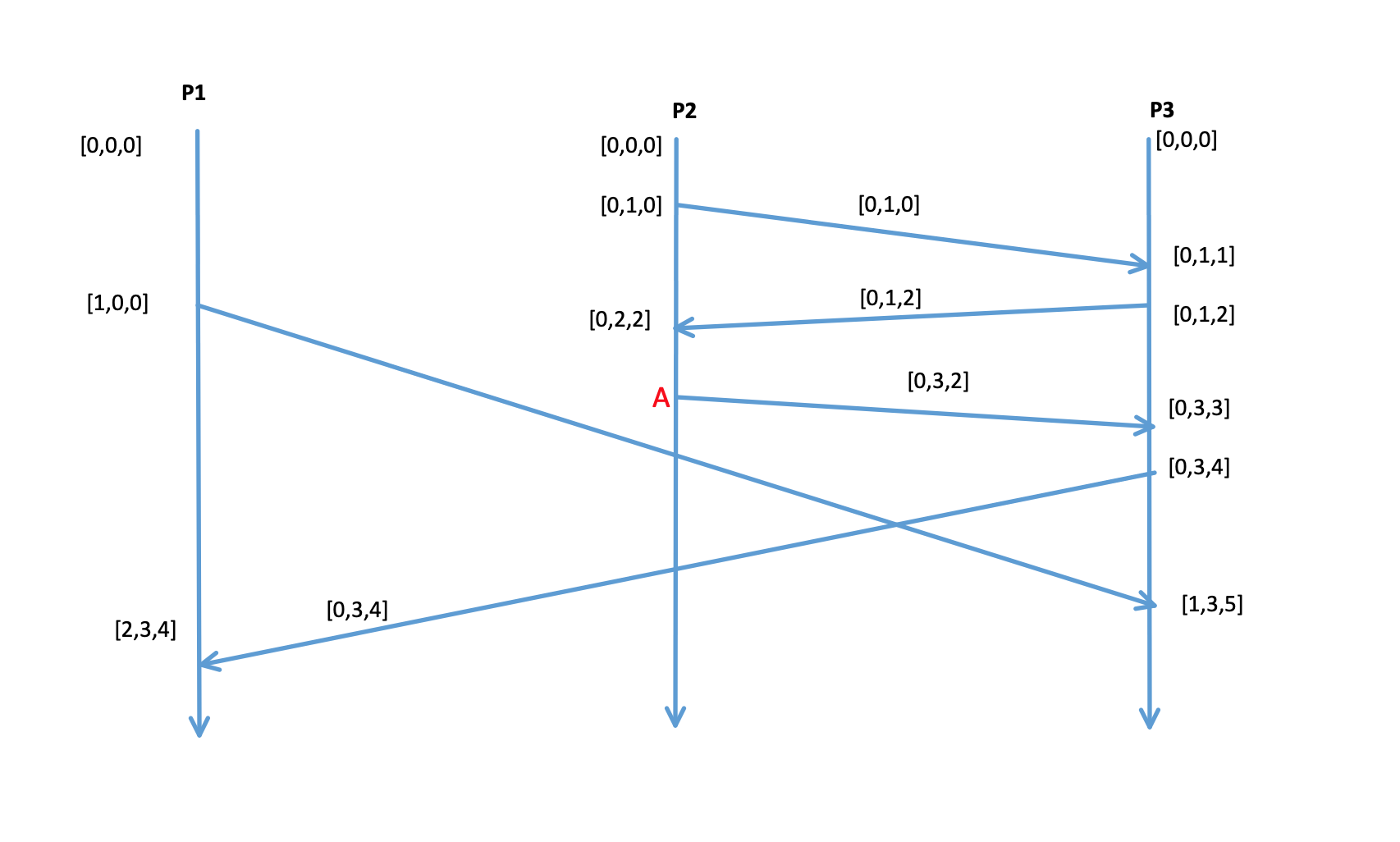
In the above system, the event A has a vector clock of [0,3,2]. Right? We can see the events that happened before A on the same process (P2). We can also say that two on P3 happened before A. Why? Second event on P3 happened before second event on P2 as it is the corresponding send-event for second event on P2. And the first event on P3 happened before the second event on P3. In general, the causal history of an event A is a set of all events which have vector clocks same or smaller than that of A on every position.
Similarly causal effects of A include all events which have VCs same or more than that of A at every position. If there is an event that has a VC with some positions as same or more and other positions smaller than VC(A), then that event is independent of A. So in above picture, the first event on process P1- which has VC [1,0,0] cannot be on the causal history nor can it be an effect of the event A. It is independent of A.

Are last events on P1 and P3- those having VCs [2,3,4] and [1,3,5] causally connected?

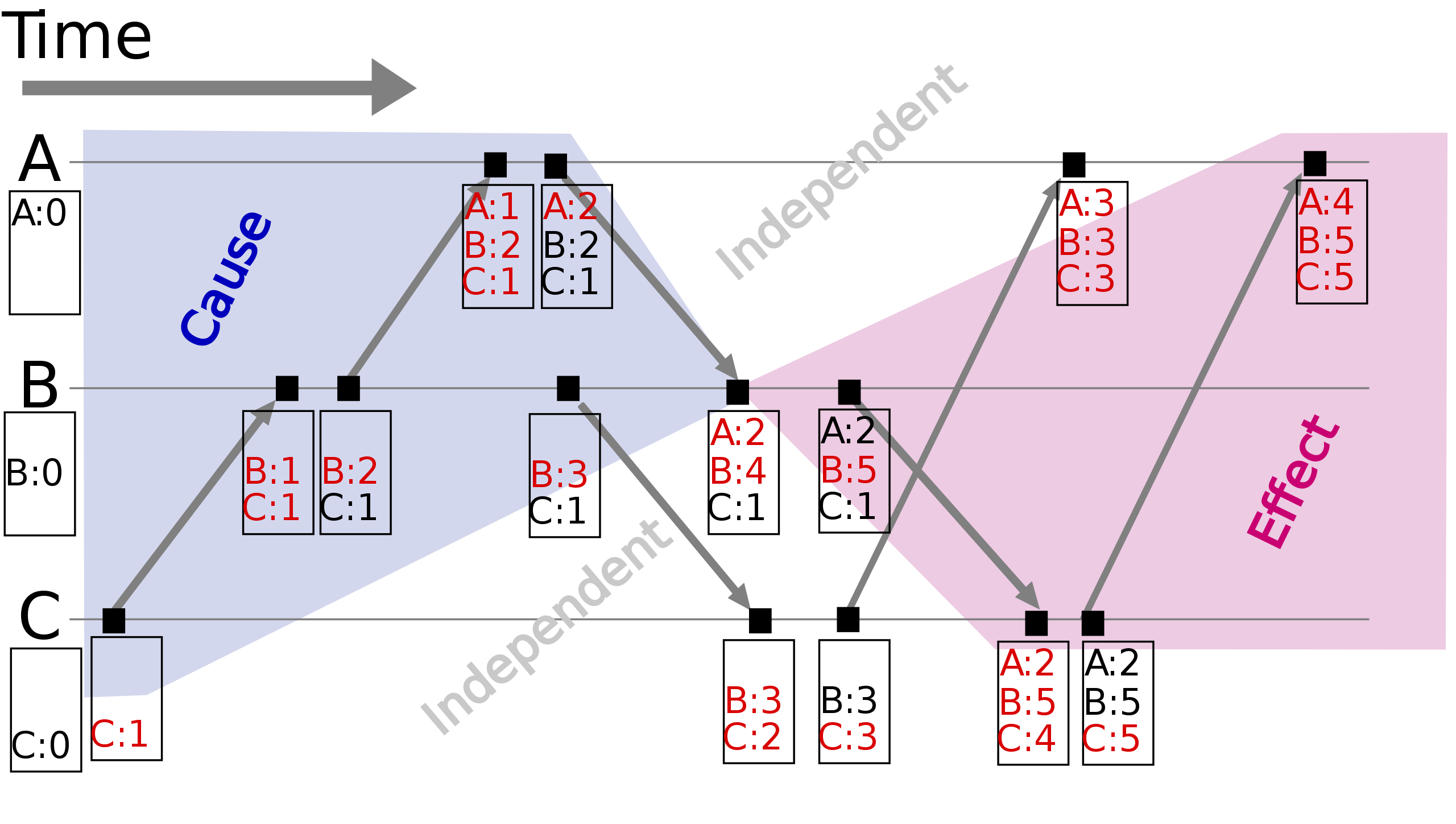
Here is an image from wikipedia showing some events causally connected to event on process B with VC {A:2, B:4, C:1} as well as some independent events.